Una definición de

Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

Una definición de $\pi$

El número $\pi$ se define como el cociente del perímetro de un círculo y su diámetro. Este es el punto de partida para establecer una definición rigurosa de este número. $\medskip$

Según nuestra definición intuitiva de $\pi$ , si se denota el perímetro del círculo con (recuerde que el diámetro es 2), se obtiene:

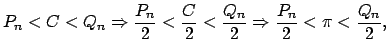$\displaystyle P_{n}<C<Q_{n}\Rightarrow \frac{P_{n}}{2}<\frac{C}{2}<\frac{Q_{n}}{2}\Rightarrow \frac{P_{n}}{2}<\pi <\frac{Q_{n}}{2},$

y tomando en cuenta la identidad (8), se debe definir:

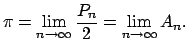$\displaystyle \pi =\lim\limits_{n\rightarrow \infty }\frac{P_{n}}{2}=\lim\limits_{n \rightarrow \infty }A_{n}.$

Lo anterior completa el análisis intuitivo que fundamenta la siguiente definición. $\medskip$

Definición: Se define

$\displaystyle \pi =\lim\limits_{n\rightarrow \infty }2^{n}s_{n}c_{n}=\lim\limits_{n\rightarrow \infty }2^{n}c_{n}\sqrt{1-c_{n}^{2}},$

donde $c_{n}$ está definida recursivamente por (3).

Nótese que

$\displaystyle \pi =\lim\limits_{n\rightarrow \infty }A_{n}=\lim\limits_{n\rightarrow \infty }A_{n+1}=\lim\limits_{n\rightarrow \infty }2^{n}s_{n}.$

Ahora que ya se ha definido $\pi$ , es importante notar que el área del polígono circunscrito es:

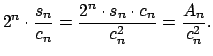$\displaystyle 2^{n}\cdot \frac{s_{n}}{c_{n}}=\frac{2^{n}\cdot s_{n}\cdot c_{n}}{c_{n}^{2}}=\frac{A_{n}}{c_{n}^{2}}.$

El área del círculo, que denotaremos por $A_{c}$ , debe satisfacer:

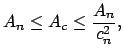$\displaystyle A_{n}\leq A_{c}\leq \frac{A_{n}}{c_{n}^{2}},$

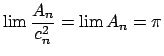y como $\lim \dfrac{A_{n}}{c_{n}^{2}}=\lim A_{n}=\pi$ , se debe tener:

$\displaystyle A_{c}=\lim\limits_{n\rightarrow \infty }A_{n}=\pi ,$

como era de esperarse. $\medskip$

Lo anterior demuestra que:

El número $\pi$ es el límite del conciente entre el perímetro $P_{n}$ y el diámetro .
El número $\pi$ es el límite del área $A_{n}$ del polígono de Arquímedes, de $2^{n}$ lados.