Área y perímetro del círculo de radio

Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

Área y perímetro del círculo de radio

Considere un polígono regular de $2^{n}$ lados, inscrito en un círculo de radio . Al aplicar el teorema de Pitágoras se obtiene la relación entre la apotema $\widehat{c}_{n}$ del polígono y la midad de la medida de su lado $\widehat{s}_{n}$ :

$\displaystyle \widehat{s}_{n}^{2}+\widehat{c}_{n}^{2}=r^{2},$ de donde $\displaystyle \widehat{s}_{n}=\sqrt{r^{2}-\widehat{c}_{n}^{2}}.$

Al igual que con $c_{n}$ , se obtiene la fórmula de recurrencia para $\widehat{c}_{n}$ :

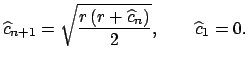$\displaystyle \widehat{c}_{n+1}=\sqrt{\dfrac{r\left( r+\widehat{c}_{n}\right) }{2}},\qquad \widehat{c}_{1}=0.$

Siguendo el mismo procedimiento descrito en la sección 4.2, se obtiene un polígono circunscrito al círculo de radio cuyo lado mide:

$\displaystyle 2r\frac{\widehat{s}_{n}}{\widehat{c}_{n}}.$

Se puede demostrar por inducción que:

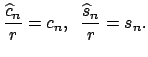$\displaystyle \dfrac{\widehat{c}_{n}}{r}=c_{n},\;\;\dfrac{\widehat{s}_{n}}{r}=s_{n}.$

Entonces:

$\displaystyle \lim\limits_{n\rightarrow \infty }\widehat{c}_{n}=\lim\limits_{n\rightarrow \infty }r\cdot c_{n}=r\lim\limits_{n\rightarrow \infty }c_{n}=r.$

Se denotan con $\widehat{P}_{n}$ y $\widehat{Q}_{n}$ los perímetros del polígono inscrito y circunscrito respectivamente, entonces:

$\displaystyle \widehat{P}_{n}$	$\displaystyle =$	$\displaystyle 2^{n}\cdot 2\widehat{s}_{n}=2^{n+1}\cdot r\cdot s_{n}=2rA_{n+1}=rP_{n}.\medskip$
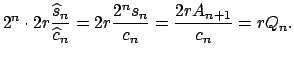$\displaystyle \widehat{Q}_{n}$	$\displaystyle =$	$\displaystyle 2^{n}\cdot 2r\frac{\widehat{s}_{n}}{\widehat{c}_{n}}=2r\frac{2^{n}s_{n}}{c_{n}}=\frac{2rA_{n+1}}{c_{n}}=rQ_{n}.$

Por (8), las sucesiones $(\widehat{P}_{n})$ y $(\widehat{Q}_{n})$ son convergentes y además:

$\displaystyle \lim\limits_{n\rightarrow \infty }\widehat{P}_{n}=\lim\limits_{n \rightarrow \infty }\widehat{Q}_{n}=\pi r$

Note que el perímetro del círculo $\widehat{C}$ debe cumplir:

$\displaystyle \widehat{P}_{n}<\widehat{C}<\widehat{Q}_{n},$

y tomando el límite se obtiene la conocida fórmula del perímetro del círculo de radio

$\displaystyle \widehat{C}=\lim\limits_{n\rightarrow \infty }\widehat{P}_{n}=\lim\limits_{n \rightarrow \infty }2rA_{n+1}=2\pi r.$

En particular, para cualquier círculo de radio , el cociente de su perímetro y su diámetro es constante:

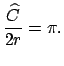$\displaystyle \frac{\widehat{C}}{2r}=\pi .$

Por otro lado, denotando con $\widehat{A}_{n}$ el área del polígono inscrito se obtiene:

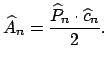$\displaystyle \widehat{A}_{n}=\frac{\widehat{P}_{n}\cdot \widehat{c}_{n}}{2}.$

y el área del circunscrito es:

$\displaystyle \dfrac{\widehat{A}_{n}}{\widehat{c}_{n}}.$

Note que:

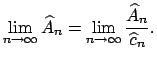$\displaystyle \lim\limits_{n\rightarrow \infty }\widehat{A}_{n}=\lim\limits_{n\rightarrow \infty }\dfrac{\widehat{A}_{n}}{\widehat{c}_{n}}.$

Entonces, el área $\widehat{A}_{c}$ del círculo de radio debe definirse por:

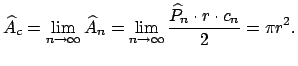$\displaystyle \widehat{A}_{c}=\lim\limits_{n\rightarrow \infty }\widehat{A}_{n}... ...\rightarrow \infty }^{{}}\frac{\widehat{P}_{n}\cdot r\cdot c_{n}}{2}=\pi r^{2}.$

Se concluye entonces que el área del círculo de radio

es $\pi r^{2}$ , y su perímetro es $2\pi r$ .