|
Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15
16 17
18 19 20
21
22 23 24
25 26
27 28 29
30 31
32 33 34
35 36
37 38
Utilizando las desigualdades e igualdades de la sección anterior se obtienen los siguientes límites.
Teorema 14
Las funciones 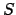 y y 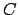 cumplen: cumplen:
Prueba
- Por el teorema anterior se tiene que
y al aplicar el teorema del encaje se obtiene el resultado.
- Del teorema anterior, se sigue que
y nuevamente por el teorema del encaje se obtiene que
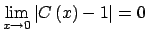 . .
- Del teorema anterior se sabe que
para
![$ x\in \left] 0,\frac{1}{4}\right[ $](img523.png) . Como las funciones involucradas en esta desigualdad son pares, esta es válida también para . Como las funciones involucradas en esta desigualdad son pares, esta es válida también para
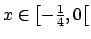 . Por el teorema del encaje se obtiene el resultado. . Por el teorema del encaje se obtiene el resultado.

Como
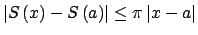 , para todo , para todo
 , entonces por el teorema del encaje se obtiene que , entonces por el teorema del encaje se obtiene que
es decir
De manera similar se obtiene
Lo anterior demuestra el siguiente teorema:
Teorema 15
Las funciones 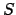 y y 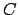 son continuas en todo son continuas en todo
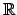 . .
|
![]()
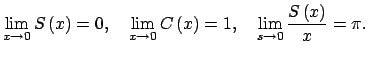
![]() , para todo
, para todo
![]() , entonces por el teorema del encaje se obtiene que
, entonces por el teorema del encaje se obtiene que