|
Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15 16 17
18 19 20
21
22 23 24
25 26
27 28 29
30 31
32 33 34
35 36
37 38
A continuación utilizaremos algunas de las fórmulas básicas de polígonos, con el fin de encontrar una manera de construir las funciones seno y coseno. 
Consideremos un polígono regular de 2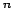 lados, inscrito en un círculo de radio lados, inscrito en un círculo de radio 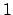 . Este polígono se divide en . Este polígono se divide en 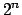 triángulos, formados al trazar todos los radios a los vértices del polígono, y sus ángulos centrales miden triángulos, formados al trazar todos los radios a los vértices del polígono, y sus ángulos centrales miden
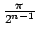 radianes. En la figura 2 se muestra un lado radianes. En la figura 2 se muestra un lado
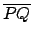 del polígono y el triángulo que forma. del polígono y el triángulo que forma.
Figura
2
Figura 3
|
|
Se observa que el triángulo  es isósceles debido a que dos de sus lados son radios del círculo, por lo tanto al trazar la altura del triángulo que pasa por es isósceles debido a que dos de sus lados son radios del círculo, por lo tanto al trazar la altura del triángulo que pasa por  , esta biseca al , esta biseca al
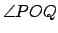 . Así se obtiene que . Así se obtiene que
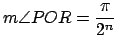 . .
Además, se nota que
sen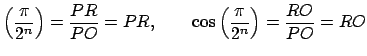 |
|
Nótese que entonces,
sen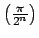 es la mitad de la medida del lado del polígono de es la mitad de la medida del lado del polígono de 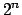 lados, y lados, y
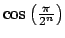 es la apotema del mismo polígono. Esta es la base intuitiva de la construcción que desarrollaremos. es la apotema del mismo polígono. Esta es la base intuitiva de la construcción que desarrollaremos. 
En adelante denotaremos con 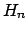 a un polígono de Arquímedes de a un polígono de Arquímedes de 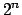 lados, inscrito en un círculo de radio lados, inscrito en un círculo de radio 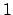 . La medida de sus lados se denota por . La medida de sus lados se denota por 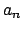 , su apotema por , su apotema por 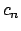 , y se define , y se define 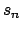 como la mitad de la medida de su lado, es decir como la mitad de la medida de su lado, es decir
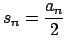 . Note que el semiperímetro es . Note que el semiperímetro es
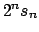 . .
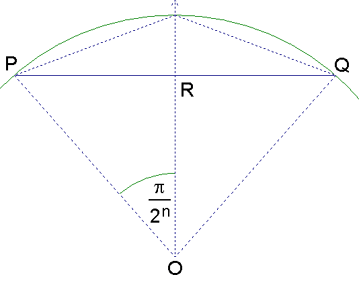
En la figura 3 se muestra uno de los lados del polígono 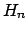 y su relación con uno de los lados del polígono y su relación con uno de los lados del polígono 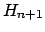 . .
Como el triángulo 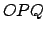 es isósceles, entonces es isósceles, entonces
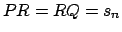 . Aplicando el teorema de Pitágoras al triángulo . Aplicando el teorema de Pitágoras al triángulo 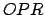 se obtiene se obtiene
de donde se obtienen las identidades:
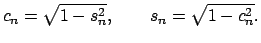 |
(2) |
|
![]()