|
Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15 16 17
18 19 20
21
22 23 24
25 26
27 28 29
30 31
32 33 34
35 36
37 38
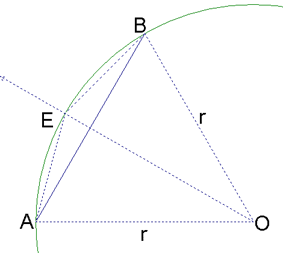
Considere un polígono regular de 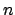 lados inscrito en un círculo dado de centro lados inscrito en un círculo dado de centro 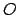 . El centro de dicho círculo es llamado también centro del polígono. Un ángulo central del polígono es un ángulo central del cículo, determinado por dos vértices consecutivos del polígono. Por congruencia de triángulos, todos los ángulos
centrales son congruentes, y por lo tanto cada uno mide . El centro de dicho círculo es llamado también centro del polígono. Un ángulo central del polígono es un ángulo central del cículo, determinado por dos vértices consecutivos del polígono. Por congruencia de triángulos, todos los ángulos
centrales son congruentes, y por lo tanto cada uno mide
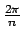 radianes. radianes. 
Considere un lado del polígono, denotado por
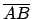 , y trace el rayo que parte del centro , y trace el rayo que parte del centro  y pasa por el punto medio de ese lado. Dicho rayo interseca a la circunferencia en un punto y pasa por el punto medio de ese lado. Dicho rayo interseca a la circunferencia en un punto  (ver figura 1.a). (ver figura 1.a).
Figura
1.a
Figura1.b
|
|
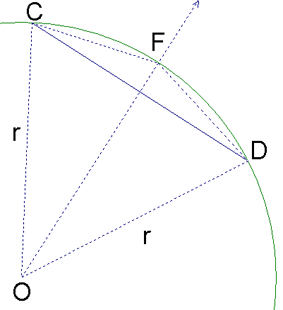
Por el cirterio 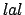 , se tiene que los triángulos , se tiene que los triángulos 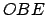 y y 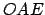 son congruentes, y en particular son congruentes, y en particular 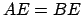 . Dado otro lado cualquiera del polígono ( . Dado otro lado cualquiera del polígono (
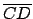 en la figura 1.b), como los ángulos centrales tienen la misma medida, entonces por el mismo criterio se obtiene que en la figura 1.b), como los ángulos centrales tienen la misma medida, entonces por el mismo criterio se obtiene que
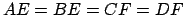 . .
De esta forma se construye un polígono regular de 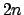 lados. Repitiendo el proceso indefinidamente, se construye una sucesión de polígonos regulares inscritos en el círculo, cada uno de los cuales tiene el doble de lados que el anterior. En adelante, estos polígonos se denominarán polígonos de Arquímedes, y al método para construirlos se le llamará método de exhausión. En la construcción a presentar, se comenzará con un cuadrado en vez de un hexágono regular, obteniendo sucesivamente polígonos de lados. Repitiendo el proceso indefinidamente, se construye una sucesión de polígonos regulares inscritos en el círculo, cada uno de los cuales tiene el doble de lados que el anterior. En adelante, estos polígonos se denominarán polígonos de Arquímedes, y al método para construirlos se le llamará método de exhausión. En la construcción a presentar, se comenzará con un cuadrado en vez de un hexágono regular, obteniendo sucesivamente polígonos de 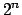 lados, para cada número natural lados, para cada número natural 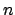 . Para la construcción es importante recordar la densidad de los diádicos. . Para la construcción es importante recordar la densidad de los diádicos.
|
![]()