|
Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15 16 17
18 19 20
21
22 23 24
25 26
27 28 29
30 31
32 33 34
35 36
37 38
Es conocido que dado un entero 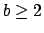 , para todo número real positivo , para todo número real positivo 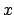 existe una expansión de existe una expansión de 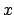 en base en base 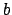 , de la forma , de la forma
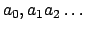 , donde , donde
![$ a_{0}=[\![x]\!]$](img45.png) , y para , y para 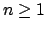 se tiene que se tiene que
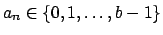 , esto es: , esto es:
Más precisamente se tiene, para cada
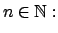
En lo que sigue se tomará 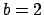 . En tal caso se habla de expansiones binarias. Además, para cada . En tal caso se habla de expansiones binarias. Además, para cada 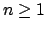 se tiene se tiene
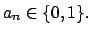 Para detalles sobre este tema, consultar [4]. Para detalles sobre este tema, consultar [4].
Dado 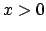 , con expansión binaria , con expansión binaria
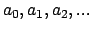 , se definen
las sucesiones , se definen
las sucesiones
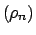 y y
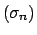 así: así:
Por lo anterior, para cada
 se tiene: se tiene:

Note que
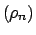 es creciente, dado que es creciente, dado que
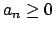 para cada para cada 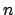 , y además , y además
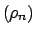 converge a converge a 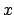 . . 
De igual forma, la sucesión
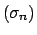 resulta decreciente, debido a que resulta decreciente, debido a que
También es claro que
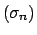 converge a converge a 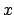 . . 
 Se define el conjunto de los Diádicos como Se define el conjunto de los Diádicos como
Cada 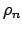 pertenece al conjunto pertenece al conjunto
 . En efecto, . En efecto,
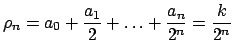 , donde , donde
Eso demuestra que todo  se puede aproximar arbitrariamente por elementos del conjunto se puede aproximar arbitrariamente por elementos del conjunto
 . . 
Mejor aún, existen sucesiones
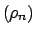 y y
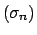 , cuyos elementos pertenecen todos a , cuyos elementos pertenecen todos a
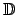 , la primera creciente y la segunda decreciente, tales que , la primera creciente y la segunda decreciente, tales que
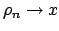 y y
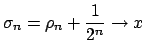 . Si . Si 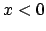 , se
puede aplicar lo anterior a , se
puede aplicar lo anterior a 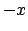 , para obtener el mismo resultado. Lo anterior se resume en el siguiente teorema. , para obtener el mismo resultado. Lo anterior se resume en el siguiente teorema.
|
![]()