|
Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15 16 17
18 19 20
21
22 23 24
25 26
27 28 29
30 31
32 33 34
35 36
37 38
Arquímedes utilizó el método de exhausión para hallar aproximaciones del número 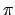 , logrando determinar que , logrando determinar que
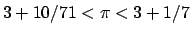 . Para desarrollar este método primero inscribió un hexágono regular en una circunferencia; posteriormente halló el punto medio de cada uno de los arcos formados por los lados del hexágono, y finalmente trazó los segmentos que unen cada uno de esos puntos medios con los vértices del lado correspondiente, formando así un dodecágono. De esta forma, duplicando sucesivamente el número de lados, llegó hasta un polígono de 96 lados. Un proceso similar desarrolló con polígonos circunscritos. Designando con . Para desarrollar este método primero inscribió un hexágono regular en una circunferencia; posteriormente halló el punto medio de cada uno de los arcos formados por los lados del hexágono, y finalmente trazó los segmentos que unen cada uno de esos puntos medios con los vértices del lado correspondiente, formando así un dodecágono. De esta forma, duplicando sucesivamente el número de lados, llegó hasta un polígono de 96 lados. Un proceso similar desarrolló con polígonos circunscritos. Designando con 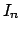 y y 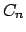 los perímetros de los polígonos regulares inscritos y circunscritos respectivamente, Arquímedes llegó a la conclusión de que los perímetros de los polígonos regulares inscritos y circunscritos respectivamente, Arquímedes llegó a la conclusión de que
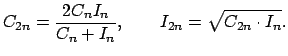 |
(1) |
Arquímedes considera el círculo como un polígono regular de un número infinito de lados, en el que la apotema se va convirtiendo en el radio. Esta consideración hace que se pueda justificar fácilmente la fórmula para el área de un círculo de radio 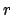 a partir de la expresión para el área de un polígono regular. En efecto, por definición se tiene que a partir de la expresión para el área de un polígono regular. En efecto, por definición se tiene que
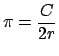 , donde , donde 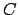 es el perímetro del círculo, así que es el perímetro del círculo, así que 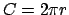 . Asumiendo que la fórmula del área de un polígono regular es válida para el círculo, se tendría: . Asumiendo que la fórmula del área de un polígono regular es válida para el círculo, se tendría:
En este trabajo, se utilizará la metodología propuesta por Arquímedes, proponiendo con base en la intuición una sucesión numérica 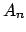 que representa el área de un polígono regular de que representa el área de un polígono regular de 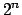 lados, inscrito en un círculo de radio lados, inscrito en un círculo de radio 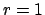 . El teorema de
Weierstrass de análisis real se encarga del paso al límite, dando rigor a las definiciones involucradas. . El teorema de
Weierstrass de análisis real se encarga del paso al límite, dando rigor a las definiciones involucradas.
|
![]()