Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15
16 17
18 19 20
21
22 23 24
25 26
27 28 29
30 31
32 33 34
35 36
37 38
A continuación se determinarán las derivadas de las funciones 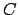 y y 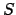 . Para la función . Para la función 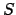 se tiene que se tiene que
Por el teorema 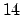 se tiene que se tiene que
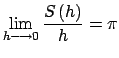 y y
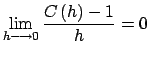 , y entonces , y entonces 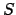 es derivable, y es derivable, y
Similarmente se obtiene que
Debido a que se conoce los intervalos de monotomía de 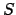 y y 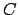 y sus derivadas estan relacionacionadas con ellas mismas, se pueden obtener los intervalos de concavidad de y sus derivadas estan relacionacionadas con ellas mismas, se pueden obtener los intervalos de concavidad de 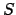 y y 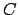 . En efecto, por ejemplo en . En efecto, por ejemplo en
![$ \left[ 0,\frac{1}{2}\right]$](img341.png) , la función , la función 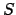 es estrictamente creciente y la función es estrictamente creciente y la función 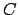 es estrictamente decreciente, entonces es estrictamente decreciente, entonces
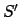 y y
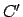 son ambas estrictamente decrecientes, y por lo tanto ambas gráficas de son ambas estrictamente decrecientes, y por lo tanto ambas gráficas de 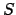 y y 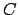 son cóncavas hacia abajo en el intervalo son cóncavas hacia abajo en el intervalo
![$ \left[2n,\frac{1}{2}+2n\right] $](img557.png) , por ser periódicas. El siguiente teorema resume los otros casos que el lector puede comprobar. , por ser periódicas. El siguiente teorema resume los otros casos que el lector puede comprobar.
|
![]()
![$\displaystyle S^{\prime }\left( x\right) =\lim\limits_{h\rightarrow 0}\dfrac{S\...
...ac{C\left( h\right) -1}{h}+C\left( x\right) \frac{S\left(h\right) }{h}\right] .$](img549.png)
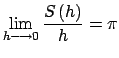 y
y
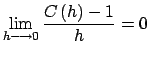 , y entonces
, y entonces