Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15  16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

 

Desigualdades importantes de $ S$ y $ C$ en $ \mathbb{R}$

El siguiente teorema tiene por objetivo extender las desigualdades obtenidas en $ \mathbb{D}$ a $ \mathbb{R}$.

Teorema 13   Para $ x,y\in \mathbb{R}$ se cumple:

  1. $ \left\vert S\left( x\right) \right\vert \leq \pi \left\vert x\right\vert $

  2. $ \left\vert S\left( x\right) -S\left( y\right) \right\vert \leq \pi \left\vert ... ...eft( x\right) -C\left( y\right) \right\vert \leq \pi \left\vert x-y\right\vert $.

  3. $ \left\vert \dfrac{S\left( x\right) }{x}\right\vert \geq \pi \left\vert C\left( x\right) \right\vert $, si $ x\in \left[ -\frac{1}{4}, \frac{1}{4}\right] -\{0\}$

Prueba

  1. Sea $ \left( \alpha _{n}\right) $ una sucesión en $ \mathbb{D}$ convergente a $ x$, por definición $ S\left( x\right)=\lim\limits_{n\rightarrow \infty }S\left( \alpha _{n}\right) $, además como $ \alpha _{n}\in \mathbb{D}$ se tiene

    $\displaystyle \left\vert S\left( \alpha _{n}\right) \right\vert \leq \pi \left\vert \alpha _{n}\right\vert .$    

    Por las propiedades de los límites de sucesiones se obtiene

    $\displaystyle \left\vert S\left( x\right) \right\vert =\lim\limits_{n\rightarro... ...tarrow \infty }\left\vert \alpha _{n}\right\vert =\pi \left\vert x\right\vert .$    

  2. Por el teorema 12 se tiene

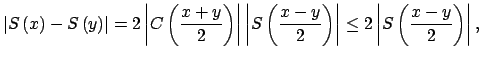    $\displaystyle \left\vert S\left( x\right) -S\left( y\right) \right\vert =2\left... ...right) \right\vert \leq 2\left\vert S\left( \dfrac{x-y}{2}\right) \right\vert ,$    

    y aplicando la parte 1 de este teorema se obtiene el resultado buscado. Para $ C$ se procede de manera similar.

  3. Sea $ \left( \alpha _{n}\right) $ una sucesión en $ \mathbb{D\cap }\left[ -\dfrac{1}{4},\dfrac{1}{4}\right] $, que converge a $ x$. Por el lema 7 se tiene

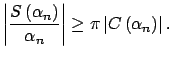    $\displaystyle \left\vert T\left( \alpha _{n}\right) \right\vert \geq \pi \left\vert \alpha_{n}\right\vert ,$ esto es $\displaystyle \left\vert \dfrac{S\left( \alpha_{n}\right) }{\alpha _{n}}\right\vert \geq \pi \left\vert C\left( \alpha_{n}\right) \right\vert .$    

    Al tomar el límite se concluye que

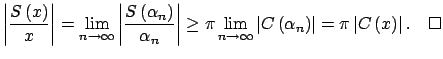    $\displaystyle \left\vert \dfrac{S\left( x\right) }{x}\right\vert =\lim\limits_{... ...{n}\right) \right\vert =\pi \left\vert C\left( x\right) \right\vert .\quad \Box$    

 

 

Revista Virtual Matemática, Educación e Internet

Derechos Reservados